Tides in Puget Sound

In a recent note I addressed the issue of correcting a barometer to sea level accounting for the tide height. The conclusion was that the barometer elevation to use is the height of the instrument above the water line plus a correction for where mean sea level (MSL) is relative to the height of the water at the time you are choosing to determine an accurate sea level pressure:

MSL correction =  ± dH + (Tide - MHW) + (MWH - MLW)/2,

where dH is the change of the draft relative to your standard waterline, which does not change much in small boats but can in larger vessels. In large vessels the reference is usually the Summer Load Line (SLL). dH can be 15 feet or more in tankers and routinely 5 ft in cargo vessels.

This correction is based on the approximation that MSL is very nearly equal to the Mean Tide Level (MTL, halfway between MLW and MHW). This approximation varies within Puget Sound from 0 to 4.5 cm, but it is plenty close enough for considerations at hand.

The task at hand now is to look at actual tide ranges in Puget Sound to show the relative significance of this barometer correction, and in doing so we learn some about how the tides vary along the length of what is often called Puget Sound, namely Port Townsend (PT) to Olympia (Oly), though this is not a strictly valid name, in that the upper portion of this water way where PT is located is called Admiralty Inlet and Puget Sound starts at the base of Whidby Island––another detail that does not matter for now.

For those less familiar with the region, here is a bathy map of the area.

 

It is about 90 nmi from PT to Oly by boat.  On the west coast of the US, we have a mixed semi-diurnal tide pattern, which looks like this at Seattle:

We have two highs and two lows and they are typically not equal, giving rise to a higher high water (HHW) and a lower low water (LLW) each day. A sample day's tide in Oly at the time of this writing is given below, which are typical values.

We can find more extreme tides in this area if we look for a new or full moon near a solstice, and without hunting for the best we can get this:

So even though we are not in Alaska, we can get high tide ranges in Puget Sound (- 4 ft to + 16 ft).  At this same time you would also get ranges of -4 to about 12 in Seattle

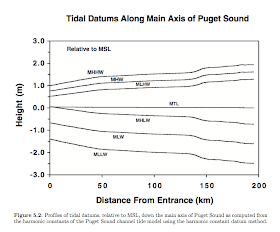
For the barometer work––and for navigation work––we need to know not just the tides but also the MHW and MLW values.  These vary along the Sound approximately as shown here:

These are numerical computations (real data below) which I show because they are already plotted!  This and other pictures presented here are from a tidal research paper called: Tidal Datum Distributions in Puget Sound, Washington, Based on a Tidal Model, NOAA Technical Memorandum OAR PMEL-122, Nov. 2002, by H.O. Mofjeld, A.J. Venturato, V.V. Titov, F.I. Gonzalez, J.C. Newman.  Their goal was to compute all of these values and compare with the tide gauge data, and they did a good job of it. 

I will show the actual numerical data at the end, but this nice plot shows what is going on.  The left is PT; the right is Oly. Again, the fact that these two places are actually only 166 km apart is not important now!

One could extract the MSL correction from a drawing like this, but the actual computation using real values is not hard, so we do not need that.  But we do see that the deeper you go into a tidal estuary, the higher the tides and the larger the correction.  This example is for Puget Sound, but you would get the same type of data going into San Francisco Bay, or Chesapeake Bay, or New York Harbor.

This plot shows that if you were doing the correction at MHH tide in Oly, you would have a MSL correction of about 2m (6.6 ft, which is 0.2 mb). At LLW it is about 2.5m (8.2 ft = 0.3 mb).

One interesting result that can be pulled from the above plot (or actual data) is shown below:

Throughout the Sound, the MSL is about 60% of the MWH, and that offers a quick way to make the correction. For example, if MHW were 10 ft and the tide is now 13 ft, then the correction is about 13 - 6 = 7 ft. In other words, if your barometer is 5 ft above the water line and the tide is 13 ft in a region where the MHW  is 10 ft, the the height you use to correct to sea level pressure is not 5 ft, it is 12 ft.  The mean sea level is 7 ft under water.

And now at this point I can imagine what might be going through the minds of the reader: Wow!  Why bother with this at all?  That is fair enough. In Puget Sound this is a small effect in all but rare cases, but we would not know that without some analysis... and we can be happy we are in Puget Sound and not near Anchorage, where the tide range can be more like 30 ft, or the Bay of Fundy at 50+ ft.

Each little bit matters if you want to do your best.  That is, if you have a good barometer that can give a dependable pressure to within a couple tenths of a mb, then we do not want to lose accuracy we do not need to––or we do not want to question our good barometer that seems off 0.3 mb at a very low tide when it had been so good in the past.  Likewise we want to know accurately the barometer height above the water line, and not just guess it.  It is analogous to the Height of Eye needed in celestial navigation sights.  Rather than guess it, take the time to measure it once then that uncertainty goes away.

For completeness, below are the actual tide data from Puget Sound and adjacent waterways.  You could piece this together from NOAA data online for any other large tidal estuary.

This compilation is from the same paper quoted above. You can disregard the two geodetic datums listed, which are not related to our discussion.  MHW and MLW are listed on most charts. There is typically a table showing multiple values for a small scale chart.