This is a way you can find UTC underway if you have lost it using only standard methods of sight reduction. This article solves the problem using a calculator solution, but this can also be worked by traditional tables and plotting with an expanded scale. The calculator used here was an early version of the StarPilot, which was developed at Starpath.
This method is often called GMT by "Lunar altitudes" as opposed to GMT by "Lunar distances." To our knowledge, the first person to describe the lunar altitude technique in modern times was John Letcher, author of a wonderful, though sadly obscure celestial nav book called Celestial Navigation with HO 208, but he is more famous for his also pioneering work on self-steering equipment. Sometime later, but independently, the technique was also described by Francis Chichester. Chances are if we look back into the last 100 years or so of of textbooks on cel nav we would find that someone else had also proposed something like this, in some form. The principle was known hundreds of years ago.
The better known Lunar Distances method is more generally applicable but it requires special sights and special analysis. The Lunar Altitudes method can be done with normal sights and normal procedures.
This post is also an experiment in digging out of the recesses of our website old articles and making them more readily available. Thus this is text from about the year 2000.
* * *
The prerequisite for the technique is a moon bearing near due east or due west at twilight. We also assume we have a watch that is running properly, but it has an unknown error in it. Our task is to use celestial measurements to determine the watch error of this watch — it can be minutes, hours, or days, but let's assume we know the day. (We have an article on how to do this we will post later.)
The simple principle of this technique is this: if we take 3 simultaneous sights, 1 each of two bodies that intersect in a good angle for a fix, and a third sight of a moon lying near due east or west, then the longitude difference between the 2-body fix and the moon's LOP is a measure of our watch error. In other words, if the watch were exactly right and we took 3 precise sights, then all 3 lines would intersect in the same place which was our true position. If the watch is wrong, the moon line will defer from the intersection of the other two, and the amount it is off is related to the watch error. Note that the latitude of the 2-body fix will be our correct latitude, even though the watch time was in error.
Example:
We have other examples of this technique worked out in our study materials and there is also one in our Emergency Navigation Book, but driving home tonight at twilight headed due east, almost straight toward a beautiful full moon, it was compelling to add a new one for users of our new StarPilot calculator. The date is Jan 19, 2000. The time is 1750 PST (ZD = +8) — but we suspect there is some error in this watch time (surprise, surprise!). Planets, stars, and a beautiful full moon fill the sky. Our DR position (also uncertain as it must be, if this is to be any challenge at all) is 47° 45' N, 123° 05'W. Our job is to figure out what the watch error is.
For this example, we will also assume that you have read through the other parts of the StarPilot description so you know more or less how it works... in other words, we will not review all the input steps here.
After taking the 6 sights listed at the end of this exercise, we plot out the results to establish what we would have obtained had we taken all 3 sights simultaneously. Naturally this cannot be done simultaneously, but if we take the series of sights 1-2-3 then 1-2-3 again, we can graph the results and interpolate a set of simultaneous values. This is a normal technique often done at sea to minimize running fix corrections. We take the moon, and two nice bright planets.
ZD=+8, WE = ? (but enter as 0 sec), HE = 9ft, IC = 0, DR = 47° 45' N, 123° 05'W, date = Jan 19, 2000, our speed = 0.
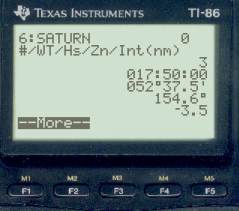
WT body Hs LOP 17:50:00 Mars 25° 04.9' a = 18.2' T 223.5° 17:50:00 Moon 19° 30.2' a = 18.7' A 081.5° 17:50:00 Saturn 52° 37.5' a = 03.5' A 154.6°
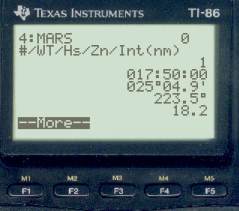
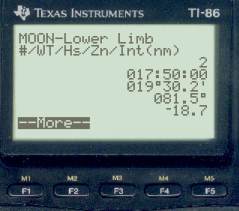
Note that the moon was indeed about due east, off only 8.5°.
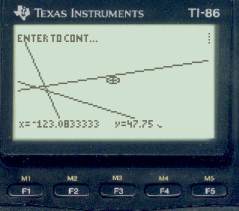
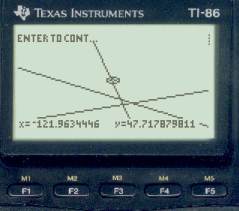
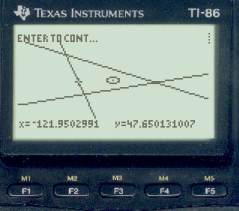
After the 3 sight reductions, we do Fix by plotting option with Speed = 0, and get the picture on the right. We will clearly have to zoom in on this to see what is going on in detail, but some things are already apparent. Our DR is far off to the east (circle in the center with the cursor in it), and we can tell already that we have a watch error — the near vertical moon line does not go through the planet fix. We also know — or you will know after you practice this some — that our watch is fast since the moon line lies to the east of the planet fix. And from the planet fix we can see that our DR lat is also too high. Remember, the lat of that intersection is correct, even though the longitude of it is clearly not correct. Now we start to zoom in by moving the cursor to the center of the LOPs as shown below top left and then press Enter and update the DR to that position and replot with a scale of 3 to get the picture next to it.
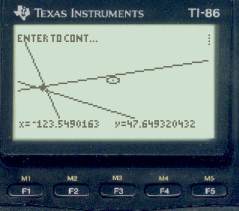
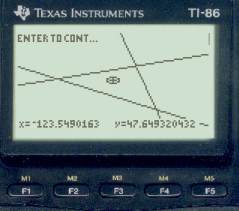
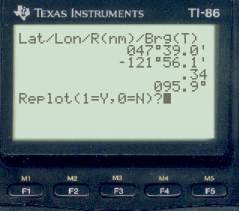
We need to know now how far east the moon line is of the planet fix, so set the cursor on the planet fix (below left) and press Enter to get the Lat-Lon of that location (bottom right). From this we see that our proper latitude is 47° 39.1 N and the longitude of this intersection is 123° 35.1' W (not our correct longitude yet since we don't know the time yet).
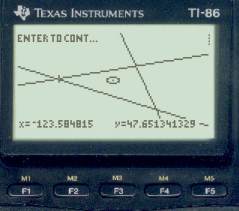

Now move the cursor to the moon line (below left) at the same Lat and press Enter to get that data as shown below right.
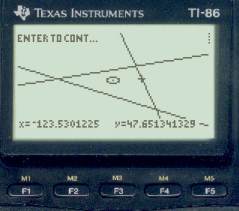
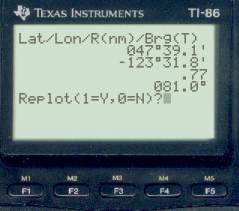
This longitude is 123° 31.8' W, which is 3.3' east of the planet fix. Our next step is to guess from this how much the watch is fast and then adjust it by that amount and do the sight reductions again. Each time we do an iteration like that we should get closer, and when all 3 lines coincide we can assume we have the right time.
Note the obvious, however, that we are assuming all sights are precisely accurate. Even a small sight error will cause a relatively large time error. And the analysis here is a bit more complicated than normal time evaluation. For example, if we do a 3-star fix that makes a nice tight triangle but unknown to us our time if off by 1 minute, the lat will be right, but the longitude will be off by 15' -- too far west if the watch is fast, and too far east if the watch is slow. But this analysis does not help us find our watch error from the moon sight.
Here we must consider that the moon is moving relative to the stars at the rate of about 360° every 30 days or 12°/day or 12x60'/24x60 min = 1'per 2 min of time. So our 3.3' discrepancy would correspond to a time error of about 6.6 minutes. Hence our first guess is that we are 6m 36s fast.
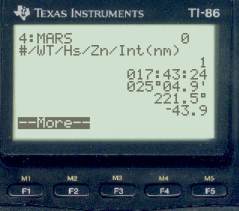
Now we redo the sight reductions at the new time of 17:50:00 - 00:06:36 = 17:43:24 WT on Jan 19, 2000. Note our DR has been stored in roughly the middle of the lines (47.39, -13.329) but it does not matter where this is for the sight reductions.
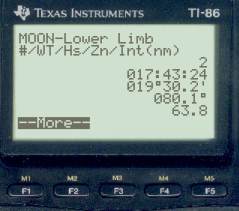
WT body Hs LOP 17:43:24 Mars 25° 04.9' a = 43.9' A 221.5° 17:43:24 Moon 19° 30.2' a = 63.8' T 080.1° 17:43:24 Saturn 52° 37.5' a = 30.1' T 151.3°
Then do fix by plot to get the screen on the right, below.

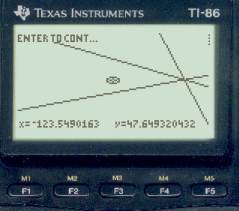
We are definitely closer on the GMT, but will need to rescale the plot to go on. Move the cursor to the center of the LOPs, update DR, and replot (left below). Then move cursor to center again, update DR and plot with scale of 6 to get right side below.
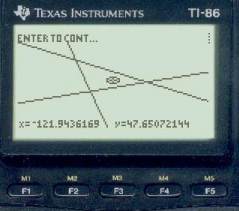
Our time correction was clearly too big, we have overshot the mark. Now lets see how many minutes too far we have gone. As before, set cursor on the fix and read the longitude, and then set cursor on the moon line at the same latitude to read it.
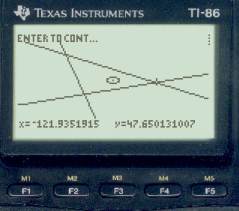

The difference is 0.9', or using our previous estimate, 0.9 x 2 = 1.8 min = 1m 48s. This would imply that our time error was not 6m 36s fast, but 6m 36s - 1m 48s = 4m 48s fast. BUT, we know from the first iteration that 2m per 1' is too big a rate. We wanted to move 3.3 and we moved 3.3 + 0.9 = 4.2. In other words, we should reduce our rate by 3.3/4.2 = 0.79. So, 1.8m x 0.79 = 1.4m = 1m 24s, and our better guess is 6m 36s - 1m 24s = 5m 12s.
So once again, redo the sights with a new time: 17:50:00 - 00:05:12 = 17:44:48.
WT body Hs LOP 17:44:48 Mars 25° 04.9' a = 09.5' T 223.4° 17:44:48 Moon 19° 30.2' a = 13.7' A 081.4° 17:44:48 Saturn 52° 37.5' a = 06.0' A 154.3°
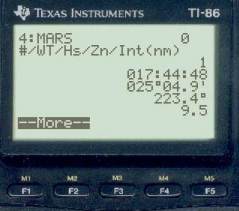
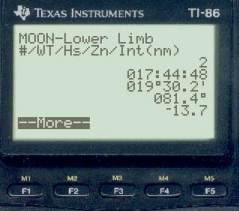

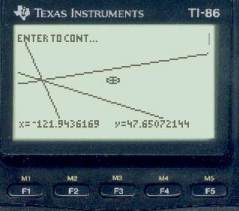
Now, again, move the cursor to the center of the fix, update DR, and replot with a scale of 10.
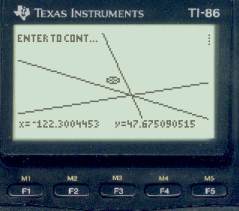
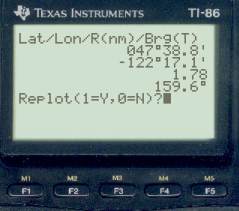
Now we are essentially done, the fix is very good now — note from the right-side screen that the range DR to fix is 1.78 miles, so this is a very tight triangle and we have found that our watch error was 5m 12s fast.
The true error was 5m exactly, so this turned out well. The main constraint on this method is it requires a moon lying near east or west at twilight. This one off by 9° worked fine. Practice with various conditions to see what the limits are. The virtue of this method is it takes only standard sights, no special sextant handling and no special computations. We just iterate the time till we get the lines to coincide.
No comments:
Post a Comment