Fit-Slope Method to Analyze Sextant Sights

We have been teaching what we named the Fit-slope Method for analysing sextant sights since 1978, and it has appeared in all of our textbooks since then. Consequently we were pleased and honored that this method was referenced in the latest edition of Bowditch's American Practical Navigator, which in turn led me to realize that we do not have an explanation of this method in public that is easy to reference, although I did post a note related to it.  That note, and the Bowditch description, are short, and do not emphasize the key aspect of the method. This note is intended to remedy that.

*  *  *

For any measurement, we always get a more realistic value by making several independent measurements and then averaging the results—or maybe even applying more sophisticated statistical analysis such as least squares.  This is no different in celestial navigation when we measure the sextant height of a star from which we can compute a line of position (LOP) on the chart. We do not want to rely on just one measurement, we want many, so we can average them in some manner.

The problem we have in the sextant measurement is everything is moving. The star is moving across the sky; we are moving across the water; and the clock hands are moving across the watch.  It is not like measuring the length of a board, where we could measure it 5 times and then average the results. In the case of the sextant height of a star, we expect it to be different every time we measure it, so we have to clarify what we mean by an average.

If we were not moving at all, such as sights on land or when dead in the water, then we only have to account for the rising or setting of the star. We will get a set of sextant heights (Hs) and specific watch times (WT). Below is an example of what these might look like when plotted as a graph.

Here we have 3 sights of a star that is descending in the sky. The vertical scale might be 5' per division with say 44º 20' at the bottom and 45º 05' at the top; the horizontal scale might be 30 sec per division starting at say 16h 20m 00s on the left and 16h 24m 30s on the right. To choose the scales, we look at the range of time and range of heights and compare that to the graph paper we have, and choose some convenient scale based on that. This type of data can also be plotted digitally with a spreadsheet (Excel and Numbers are popular commercial versions; Libre Office is a free version), and some cel nav programs like our own StarPilot do these plots automatically.

Over the duration of typical sight taking sessions (20 minutes or so), most celestial sights will follow a near linear path (meaning change in height per unit change in time is constant), providing the celestial body is not crossing our meridian at the time. So our first step analysis without further information is to just draw a line through these points using a manual form of least squares fitting. Namely the line should go through as many points as we can, leaving roughly the same number above the line as below—and maybe ignoring ones that are anomalously off the line as they are likely blunders. With little practice, navigators can actually draw this  "best fit line" as well as a computer program could using a least squares analysis.

When we choose where to draw that straight line, we have two degrees of freedom. We can move the line up and down on the page, and we can tilt the line, which is equivalent to changing its slope. The dotted line above is one choice of best fit. Once a best line is chosen, we can then choose which value will represent the "average" of the sights taken. If the line goes right through one of the points, then we can use it, and that single one will represent an average of all of them.

On the other hand, if our best line does not go through one of the actual sights, we can choose any convenient point on the line and use that for the representative average, as shown in the figure below. In these cases we might choose a point at a whole minute to simplify the later analysis. In the figure above this would be using Hs1 and WT1 to represent the average of all 3 sights, even though we did not take an actual sight at that time. With 5' per vertical interval, we then have to accept that the three sights are about ± 2' off of this average.

All of this procedure described above is what we might call standard practice, and something equivalent to this is used in most cel nav programs. This standard method, however, does not take advantage of all we know about the sights, and as such it often means we are giving up accuracy in our fix that we do not need to give up.  With that in mind,  let's look at the data again.

As we shall see, having just 3 sights is not optimum; we are better off with 4 or more, but with just three it is easier to see the point at hand.  For now we assume the slope is linear, which it is in most sight sessions—and if not, we will be able to know that as we show later. With a linear slope, we can look at these sights as the first two being consistent, and the third one being off.

Or we can think of the last two being consistent and the first one being off.

Or the first and last are consistent, but the middle one is off.  The difference between these conclusions is the slope of the data, meaning how fast does the height of the star change with time as viewed from our location. This slope also depends on the motion of our boat because that changes our position, but we will come back to that detail.  For now, we just assume we are on land or dead in the water.

This brings us to the whole point of the Fit-slope Method.  This slope is not a degree of freedom we have to vary when choosing the best line. We can easily compute this slope and then force our line to have the right slope. In other words, in the three interpretations above, only one is right. We just have to take a few minutes to figure out which one it is.

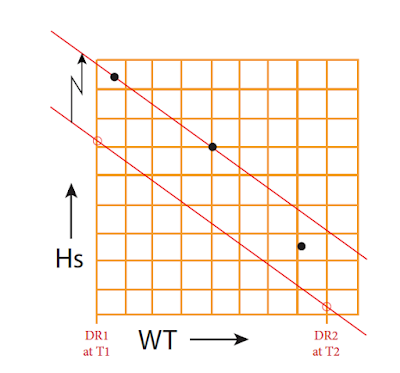
To do this, we perform standard sight reductions of the body sighted at times (T1 and T2) just before and just after the sight session, using the corresponding DR positions. This tells us what the heights (calculated height, Hc) should be at these specific times. We also get the azimuth, Zn, but we do not use that. These two Hc values can be plotted on the same plot as our data using an offset scale for the heights.  The Hc heights won't line up with Hs heights because Hc and Hs differ by all the standard sextant corrections (index, dip, and altitude). Once the two Hc values are plotted, we can see what the right slope should be.

This special determination of Hc values for the slope is best done by computation rather than using sight reduction tables. This way you can get Hc from the exact DR positions you were at times T1 and T2, which is what we need for finding the most accurate slope. You can compute Hc with a trig calculator using the basic definitions of the navigational triangle, or use a program such as the free Celestial Tools by Stan Klein. If you are online you can get Hc from the USNO—use our shortcut link starpath.com/usno. I would mention using our own commercial product StarPilot, but this step is not needed in that program as it solves the Fit-slope Method automatically.

You can if needed compute the Hc with tables alone (no computers,  no calculators), but it is extra work. Most sight reduction tables in common use require employing an assumed position, which can be as much as 30 miles away from your DR positions. The resulting Hc values are perfectly good for getting an accurate LOP, but the time slope between these two Hc values at different assumed positions is not accurate enough for what we want.

Once we have the slope plotted as above we can use parallel rulers or a roller plotter to move it up into the data to find the best fit.  We are still doing a "manual least squares" fitting by eye, but now the slope is not a variable. In many cases, this helps us rule out certain sights. In this schematic example, sight C is most likely not right, and we are likely best to just average A and B and use that to represent the set of all three. When there are 4 or more sights, the confidence in choice of outliers is more satisfying—or we learn there are no obvious outliers, and we use the spread of differences from the slope line as a measure of our uncertainty in that sight.

This procedure is not a magic bullet in any sense. It is simply imposing onto the data a property that we know (the slope) and using it to help us choose which sights might be less reliable. It is not guaranteed that the conclusions will be right, especially when there are few sights and the spread in values is not large.  But this method does give us a bit more confidence in our choices.

Since we are looking for small differences, it is important when we compute the Hc values to use the right DR positions, which will change during the sight taking session. In class we teach that each sight session starts below decks with a recording in the logbook of the time, log, course, and speed.  Then after the sights are completed, we return to the logbook and record the ending time, new log, and again record course and speed. We can use that information to mark the starting and ending DR positions on the DR track that is already plotted on our plotting sheet.  We had to have that track plotted to predict the time of the sights, and we use it again to choose a DR position for the sight reductions. (See Notes on DR and Sextant Sights.)

To show the influence of this, consider we are sailing 6 kts toward the south, taking sights of a body toward the south over a period of 30 min. Bodies near due south are crossing our meridian, so their height is not changing much with time if we were not moving, but sailing toward it we would raise its sextant angle by 3' during the 30 minutes we are sailing toward it at 6 kts.

Below is an example fix using the fit-slope method. It is from the book Hawaii by Sextant, analyzed with StarPilot. Sights are from a 1982 race, Victoria, BC to Maui, HI, near the end of the race approaching land. No other navigation was available at that time but cel nav. There was a radio beacon there, but it was not helpful for RDF at the time.

Figure 1. Raw sight data of Problem 27. C=232T; S=7.6

Notes from the book: "We are getting close to sighting land. This could be our last chance for a good fix. We do a set of morning star sights. Usually in star sight sessions we add Polaris whenever we have time to do it because it takes no pre-computation. Just set your sextant to your latitude and look north. But in this case it was woven right into the set of all sights, which were alternated in time to get the best fix."

Here is what these sights look like after they have been reduced using a calculator.

Figure 2. Analysis of the sights

This analysis does not take into account the motion of the boat. They are all reduced from the DR given in the Polaris sights. Each is valid at the WTs shown.  Below we plot all of these, adjusting each sight to the time of the last sight using Speed = 7.6 kts and Course = 232 T.

Figure 3. Plot of all sights, adjusted for boat motion. In the StarPilot, the individual LOPs are identified with a mouse cursor rollover.

The light gray vertical and horizontal lines are meridians and parallels, which end up at unusual spacing in the StarPilot plots. Here the two latitude parallels are separated  by 40.9'.

Figure 4. Showing bad Capella sight is way off the slope line (22.7' off) and can be discarded—although we did not need the fit-slope method to know this one was bad.

We see immediately that one of the Capella sights is way off and certainly a blunder, leaving us to look at the other three. Likewise, Vega has one sight notably off the others.  There is not much we can do with the Polaris data as there is no significant slope to its motion. Below are a couple of the fit slope plots.

Figure 5. Capella sights. After discarding the bad sight, the last 3 have more information. Relative to the second two, which are close to the line, the first is clearly higher. In this case, however, the difference off the line is under 1.0' so we probably won't get much difference in the fix from using the last two only or all three. 

Figure 6. The 3 Vega sights. The second is off the slope of the other two by 4.1', which we had indication of from the plot of all LOPs. So for this sight, we choose the average of the first and last as likely the best average for these 3 sights. Without the known slope line, you would have the conditions discussed in the introduction, namely not know if 2 and 3 were right, leaving 1 high, or if 1 and 2 were right, leaving 3 very high. 

Now we can redo the plot of all LOPs employing the choices from Fit-slope and again correcting for vessel motion. This is shown below.

Figure 7. Plot of all sights corrected for vessel motion. Each LOP shown represents the average of multiple sights guided by the fit-slope analysis. This is Problem 27 in Hawaii by Sextant.

My experience is that this method generally improves the fixes from typical sights at sea. In some cases, the choices of best sights to use are obvious. In other cases, we have to look at the full set of sights combined with other sights to help us make a choice.  The method is likely of most value in helping set a confidence level on the fix. If we have four sights and three line up well, but one is off, but just by, say, 1.5', then in many cases we might not feel confident to throw that one out, but with the other three nicely on the line and that one off by that much, we are more confident to remove it. This operation can then leave us with a tighter fix with less uncertainty.

Our book Hawaii by Sextant is one way to practice the method as there are many real sights and fixes included. It can certainly be tested on land, and indeed used by those new to sight taking to help evaluate their sights. You can apply it to a set of sights using a shoreline on the other side of a lake, or use it with an artificial horizon. The application of the method will be good training for actual sights at sea.
______________

To get the ultimate accuracy from a set of sights then requires us to analyze the triangle of 3 LOPs to find the best location, or most likely position, based on the shape and size of the triangle of intersections ("cocked hat"), as well as the standard deviation or variance we assign to each LOP in the set. Often these variances are the same, but when they are not, it affects the best choice.

One of the key outcomes of the fit-slope method is a better feeling for the uncertainty in an LOP based on the analysis of the several measurements we made to get the LOP.  In the above discussion, if we had done no analysis, we would have to assume something like ± 2' for the variance of this LOP, based on three measurements, not counting other information that might affect this value.  After the fit-slope analysis, this variance can be fairly reduced to about half of that, or better.

We have a related discussion called:  Most Likely Position from Three LOPs.