Please note: this rowboat exercise is unique, but the problem itself is realistic and standard. Imagine, for example, that we change to sailboat, and consider the wind calm over the current (often in the doldrums) with a motoring speed of 6 kts, and then we put NE and SE trades on either side of the current belt and set sailing speeds to match the vessel. The same types of current reckoning would still have to be carried out.
The challenge here is to find the best method to cross assuming the only goal was to get to the finish line in the shortest time. There are often other factors in practical navigation situations. Also to be a bit more realistic, we have to consider that anywhere on the line that is equal distance from Cairns is a valid answer. In other words, the finish line is not a point, but indeed a line.
The geometry is shown below, with the solution for no current. Rowing straight across along the RL.
With no current, we would stay on the RL and cross in about 350 h from 300 nmi off (14 days 14 hr). You can figure the length of the RL in current (400 nmi) from plotting, or by noting it is a side of a 30º right triangle that has sides 1:2:sqrt(3). The bottom side would then be 173 nmi.
We now look at various choices on how to cross, in no particular order. Later we come back to ask if there is a guiding philosophy that might lead us to the best solution directly. Also for now we just look at the routes and the answers. I will add a video to this that explains the solutions and how to obtain them both graphically and numerically... and the really easy way, pull out the StarPilot that calculates all these solutions directly.
Also before getting into any details, I want to stress that all of the geometry and vector problems can be solved directly by plotting on a chart or with the use of a charting program, such as OpenCPN, which is a free product. Although we illustrate the math solutions, you can indeed solve any one of these with simple plotting on a scaled sheet of paper.
Rose Point Coastal Explorer is a convenient echart program for this operation, primarily because of the way it labels the lines, and because it lets you draw a range and bearing line and then move it as you would with parallel rulers—a very convenient feature. Below is a sample of this.
Sample plot from Coastal Explorer. The current band is marked by two bearing lines, 200 nmi apart, and the rest of the solution is a combination of route lines and bearing lines.
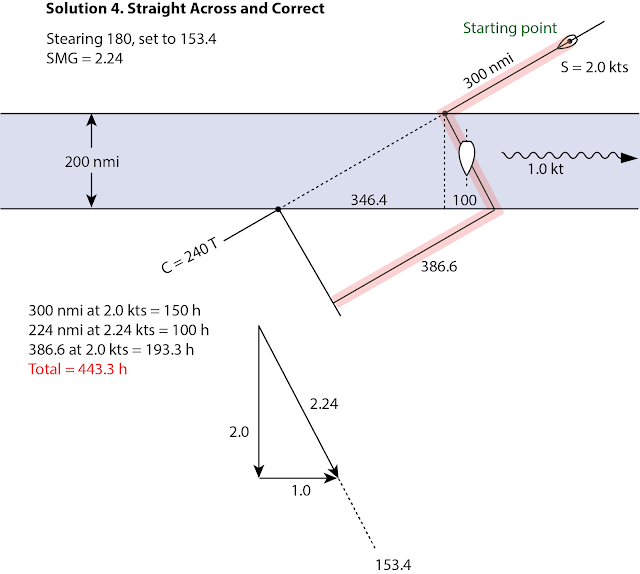
In the following approach we just steer the RL till we hit the current and then keep on steering that course knowing we are going to get set and then keep on that heading when we emerge from the current and stop the clock when we are equal distance to Cairns. The fact that we are now a bit south of where we were without current does not matter as it is the same distance to Cairns. It is not part of this analysis, but we could be better off a bit south. In any event, we get our first current crossing time, which is 436.4 hr.
Next we look at the crossing that drives down the RL till we hit the current, then we point into the current by the calculated angle that will keep us on our RL track. In other words, we can make good 2.0 and we ask how much do we have to point into a 1-kt current flowing toward 090 in order to achieve a CMG of 240. And then, when doing that, what will be our SMG as we cross?
These are standard navigation questions, which I will answer in the video. The related sketches are shown here, but only discussed there.
This turns out to be a terrible choice for crossing this current. The total time is 523.8 hr. We already know one better way, and we will keep looking. Again, refer to the forthcoming video for a review of the current solutions.
With that result in mind, we might try crossing the current in the fastest way by heading due south across it when we hit it. Then back on the RL to the finish line. That solution is shown below. We beat crabbing across by a lot, but not as good as driving across on the RL heading.
Another approach might be head up stream enough that when we get set back crossing we end up where we want to be. This is loosely called kayaker, as I recall using this method in a kayak when i did not want to compute things underway. We know the set will be 100 nmi, but we still have some geometry to solve to know what the right heading is to get there and the distance that is (772 nmi). Again easily solved by plotting and we cover the trig in the video.
This method does seem a bit extreme and indeed it does not offer a competitive time (461 hr). But it does bring to mind a compromise which is a combination of previous attempts. Namely We head up stream till we are above where the RL exits the current band, then we crab due south the RL.
Unless I have made some mistakes here, or have simply not found the best approach yet, this solution shown below seems to be the best generic solution, with a total time of 427.6 hr. Heading farther west is likely wrong considering previous solutions, but there could be some intermediate point (say 150 nmi up stream instead of 346.4) that could be faster still. Note, too, that even if the target were the point where the RL exits the current band, rather than anywhere on the finish line, this would still be the best solution.
We see quite a range of solutions, which brings us back to the question of are there guiding principles that might tell us the answer to such questions. It can be set up mathematically and the minimum solved for. But it would be more rewarding to think of a guiding principle that points us to the right solution.
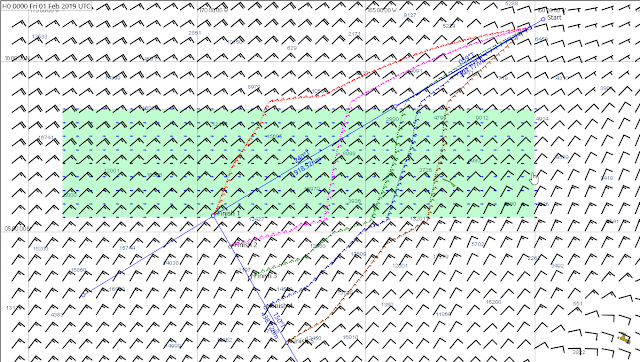
The popular routing program Expedition can in principle solve this, though it is not designed for this type of navigation. Below is an attempt to do this routing, using a unique feature of Expedition that lets us build a custom current field in GRIB format. Then I made a polar diagram that has boat speed of 2 kts regardless of wind speed or direction, and executed the route to several places along the finish line.
The routes are all within 10 hr or so, but the clear winner is the green one. Namely, row up to the current edge along the RL, and then crab across. We are still trying to understand why it chose the crab angle it did—or implies it did—but this motivated us to try something similar; RL then crab due south across the current, and then back to RL to the finish line. That is shown below.
and sure enough that is the fastest solution so far—and indeed a simple concept. We are still standing by for some feedback and checks on our solutions. However, we are homing in on a philosophy, namely follow the RL and take the most direct path across the current.
Crabbing across the current, which is pretty much the only technique discussed in standard textbooks, is likely the slowest solution in all cases. It should probably be reserved for navigating dangerous waters where you must stay on a particular track for safety sake. We will follow up on this with some realistic current crossings on inland waters to see how far we can go with this idea.







2 comments:
Thanks for posting this. To recap: Follow RL to edge of current; establish COG that is 90 degrees to current and cross; once across, take shortest path to destination.
Thanks! That's worth knowing.
Fred
Drat.
When David's solution post clearly showed that my intuition was wrong, I cobbled together some Python - calling it a program would be generous - to explore the parameters. I was able to nearly duplicate David's solutions for cases 2-6 (my values are close enough that I think the differences are rounding differences).
Then I ran some other values, and I believe - my math isn't very trustworthy - that Solution 7 can be slightly improved with a stream crossing course steered of 217°. I think this brings the total time down from David's 415.6 (or my 415.5) to 414.19. This is utterly trivial if you are rowing, but sadly contradicts the appealing idea that the fastest solution has a course made good perpendicular to the stream.
Post a Comment